Bayesian Regression for Nonlinear Models
This project was an introduction to the use of sampling methods in order to perform statistical analysis on a distribution that has no closed-form analytical expression. The implementation for this project consisted of Metropolis Hastings MCMC, Adaptive MCMC (AM), Delayed Rejection MCMC (DR) and Delayed Rejection Adaptive MCMC (DRAM) in order to sample from a posterior distribution obtained from performing inference on parameters of a nonlinear model.
Relevant Skills and Topics:
Bayesian Statistics
Nonlinear regression
Python
Bayesian Inference and Conjugate Pairs
Bayesian inference is a method in order to update the belief as evidence pertaining to the thing to topic/parameter is introduced. At its bare-bones form, Bayesian inference uses Bayes’ Rule, which describes a posterior distribution (the belief represented upon observing evidence/data) as a combination of a likelihood, a prior belief and the evidence.
Bayes’ Rule, posterior P(Θ|D) expressed in terms of the likelihood P(D|Θ), the prior P(Θ) and the evidence P(D). Sometimes written as the second line, as the evidence is difficult to compute; hence, the posterior is proportional to the likelihood and prior.
This is perhaps one of the more intuitive outlooks on the concept of learning from data: The amount that you learn from information that you gain is proportional to your prior information on the topic, and how the new information you gain matches the prior information you have.
The posterior distribution represents our belief after we update on new information we obtain. This distribution, in statistical analysis, is typically in the form of a probability density function (PDF). The most widely known and used PDF is probably the one belonging to the Gaussian distribution, which has a nice analytical expression. In the case where you have an analytical expression like a Gaussian as your posterior, computing the statistical properties is somewhat simple. It is worthwhile to also mention the concept of conjugate priors, where the family of distributions for the prior belief and posterior are the same under a linear model. This means that under some linear transformation induced by your model, a distribution will remain under the same family of distributions,
Nonlinear Models and Posterior Analysis
When there is a nonlinear model, unfortunately the conjugate priors do not apply - so if you have some expression for the prior distribution for a parameter that you then update the belief on according to a nonlinear model, the posterior will not be in the form of the same family of distributions.
Due to the lack of an analytical expression of the posterior distribution, sampling from it then becomes extremely difficult. It is similar to trying to guess what the shape of an object is, without knowing much about the object itself - nearly impossible without a very good guessing method!
Markov Chain Monte Carlo (MCMC)
The MCMC algorithm is one of the best established and researched algorithms for sampling from an arbitrary distribution. It essentially makes a guess according to a random walk and evaluates how likely it is that that point lies on the target distribution. This evaluation is the acceptance probability of that point being on the target distribution. If accepted, the next guess is made according to that point, if not, according to another point from the result of a random walk point from the previous point.
This algorithm follows the properties of the Markov chain, such that the next proposed sample relies only on its previous sample. As such, it is desired that there is low correlation across the samples that are generated. If there is high correlation, this is an indicator of the Markov property not holding and that the sampler algorithm needs tuning or a better starting point to start the “guesses” from.
An animation of how this process works is provided in the visualization section of this webpage!
Implementation
This project was for the course AEROSP 567: Statistical Inference, Estimation and Learning, taken in the first semester of my MS program. The task was to perform inference on parameters of a nonlinear Susceptible, Infected and Recovered (SIR) model, based on noisy data regarding the number of infected people from a certain infection.
The project implemented Metropolis Hastings MCMC, which is the algorithm described above. In addition, the following were implemented:
Adaptive Metropolis MCMC: A variant of the MH-MCMC, where after a certain point into the sampling process, the associated covariance of the proposal distribution is adjusted according to the covariance of the previous sample that is generated, This drastically improves the acceptance probability of the next proposed sample, as the lower uncertainty means that the next samples will not be proposed at a very far point.
Delayed Rejection MCMC: If a sample is rejected, perform a random walk sampler from the original point again, only with a smaller covariance as to decrease the probability of getting rejected.
Delayed Rejection Adaptive Metropolis MCMC (DRAM): Combination of the two.
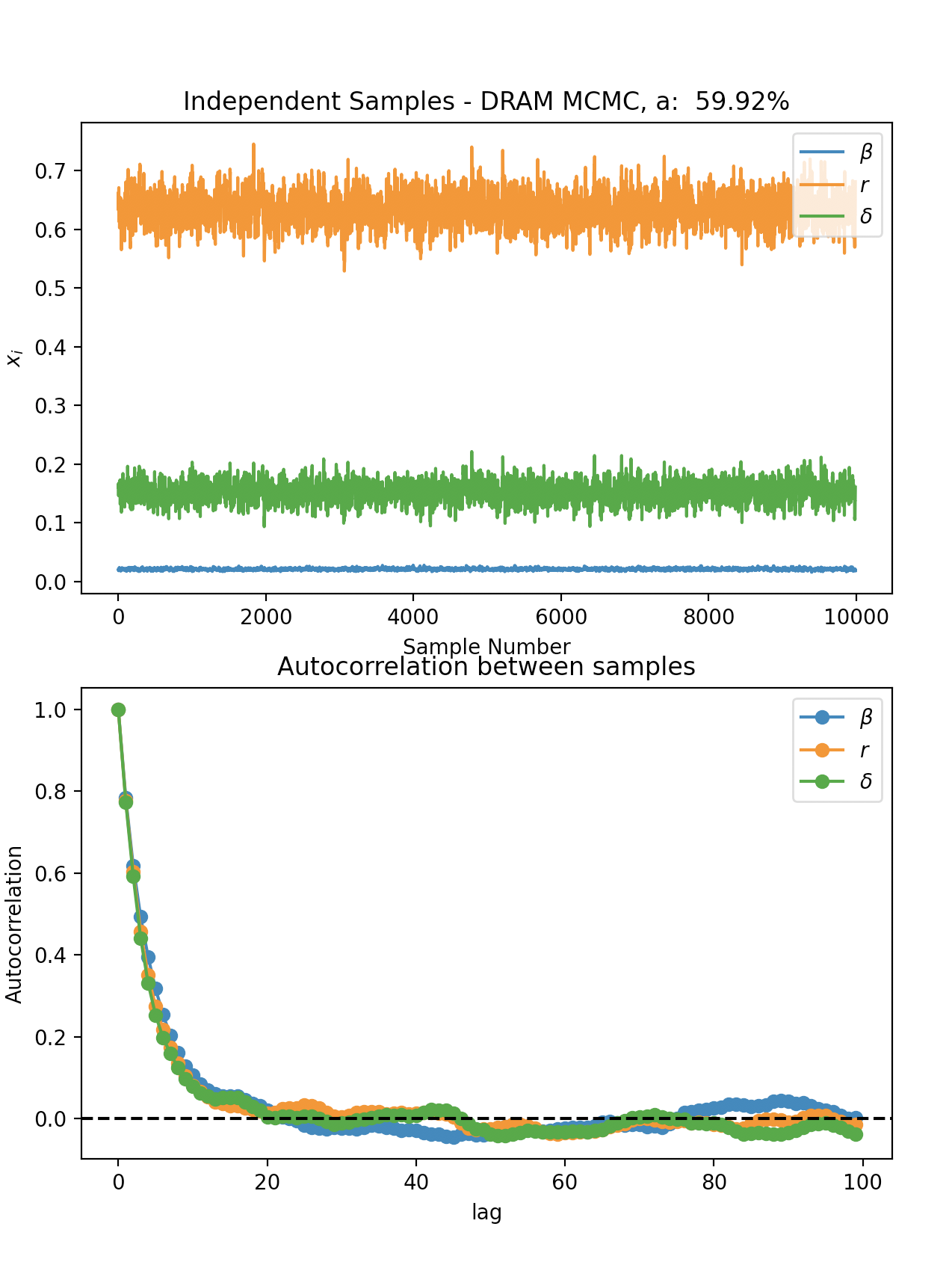
Correlation between samples and autocorrelation metric over a lag of 100, indicating a good sampling process
Posterior distribution of the parameters for the SIR model
Model representation after regression on model parameters